리만 가설이란?
리만 가설(Riemann Hypothesis)은 수학의 정수론과 복소함수론에서 가장 중요한 미해결 문제 중 하나입니다. 1859년 독일의 수학자 베른하르트 리만(Bernhard Riemann)이 제기한 이 가설은 복소수 평면에서 리만 제타 함수(ζ(s))의 모든 비자명 영점(non-trivial zeros)이 실수부가 1/2인 직선(임계선, critical line) 위에 존재한다고 주장합니다.
리만 제타 함수는 다음과 같이 정의됩니다:
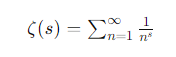
여기서 ss는 복소수입니다. 이 함수는 1보다 큰 실수 부분에서 수렴하지만, 해석적 연속(analytic continuation)을 통해 모든 복소수 평면으로 확장될 수 있습니다.
리만 가설의 중요성
- 소수 분포와의 관계: 리만 가설은 소수(prime number)의 분포와 깊은 관련이 있습니다. 리만 가설이 참이면, 소수 정리와 관련된 많은 중요한 결과가 강화되며, 소수의 분포에 대한 정확한 예측이 가능합니다.
- 정수론의 발전: 리만 가설은 소수에 대한 연구뿐만 아니라 정수론 전반에 걸친 많은 문제에 영향을 미칩니다. 수학자들은 리만 가설을 사용하여 정수론의 여러 난제를 해결하고 더 깊은 통찰을 얻을 수 있습니다.
- 해석적 수론: 리만 가설은 해석적 수론(analytic number theory)에서 중심적인 역할을 합니다. 해석적 수론은 소수와 관련된 여러 함수의 성질을 연구하며, 리만 가설은 이 분야의 많은 결과를 뒷받침합니다.
리만 가설을 해결할 경우 얻는 이점
리만 가설이 해결된다면 인류는 여러 방면에서 큰 이점을 얻을 수 있습니다.
- 암호학: 현대 암호학은 소수의 큰 수를 기반으로 하는 알고리즘에 의존합니다. 리만 가설이 참이라는 것이 입증되면, 소수의 분포에 대한 이해가 더욱 정교해져 더 안전한 암호화 알고리즘을 개발할 수 있습니다. 또한, 리만 가설이 참이라면 현재의 암호화 기법에 대한 새로운 공격 방법을 발견할 수도 있습니다.
- 소수 정리와 소수 분포 예측: 리만 가설이 참이라면 소수 정리와 관련된 여러 예측이 더 정확해집니다. 이는 소수의 분포를 예측하고, 큰 소수를 찾는 방법을 개선하는 데 도움을 줄 수 있습니다. 예를 들어, 소수 찾기 알고리즘의 효율성을 높이는 데 기여할 수 있습니다.
- 수학의 다른 분야에 미치는 영향: 리만 가설의 증명은 정수론뿐만 아니라 조합론, 대수기하학, 동역학 시스템 등 수학의 다른 분야에도 큰 영향을 미칠 수 있습니다. 수학의 다른 난제들을 해결하는 데 중요한 단서를 제공할 수 있습니다.
- 물리학과 공학: 수학의 기초가 되는 이론들이 물리학과 공학에도 영향을 미칩니다. 리만 가설이 해결되면 수학적 모델링의 정확성이 높아지고, 이는 물리학과 공학 문제를 해결하는 데 도움이 될 수 있습니다. 예를 들어, 양자역학에서의 파동 함수 해석, 신호 처리에서의 주파수 분석 등이 있습니다.
- 금융 공학: 금융 공학에서도 리만 가설의 해결은 금융 모델의 개선에 기여할 수 있습니다. 금융 시장에서의 리스크 관리, 옵션 가격 결정, 포트폴리오 최적화 등에서 사용되는 수학적 모델이 더욱 정교해질 수 있습니다.
결론
리만 가설은 수학자들이 중요하게 생각하는 문제 중 하나로, 정수론과 해석적 수론에서 중요한 역할을 합니다. 리만 가설이 해결된다면 소수 분포에 대한 깊은 이해를 바탕으로 암호학, 금융 공학, 물리학, 공학 등 여러 분야에서 혁신을 이룰 수 있을 것입니다. 이는 인류의 지식과 기술 발전에 큰 기여를 할 것으로 기대됩니다.
(시뮬레이션 우주론과의 관계)
리만 가설은 주로 수학의 정수론과 복소함수론에 속하는 문제이지만, 그 영향력은 물리학, 특히 이론물리학과 우주론에도 미칠 수 있습니다. 리만 가설이 시뮬레이션 우주론과 어떤 관계가 있는지 이해하기 위해, 몇 가지 중요한 개념을 살펴보겠습니다.
리만 가설과 물리학
리만 가설은 소수의 분포와 복소수 평면에서 리만 제타 함수의 비자명 영점(non-trivial zeros)의 성질을 설명합니다. 이는 수학적 개념이지만, 물리학에서도 응용될 수 있습니다. 특히, 리만 가설은 통계역학, 양자 혼돈(quantum chaos), 그리고 진동과 관련된 문제에서 중요한 역할을 합니다.
- 양자 혼돈과 리만 제타 함수: 양자 혼돈 이론에서는 리만 제타 함수의 비자명 영점이 양자 시스템의 에너지 준위와 유사한 성질을 가진다고 알려져 있습니다. 이로 인해 리만 제타 함수는 양자 물리학의 모델에서 중요한 역할을 할 수 있습니다.
- 물리학적 모형: 물리학자들은 리만 제타 함수의 성질을 이용하여 다양한 물리학적 현상을 모델링합니다. 예를 들어, 통계역학에서 리만 제타 함수는 특정 시스템의 에너지 상태와 관련된 분포를 설명하는 데 사용됩니다.
시뮬레이션 우주론과의 관계
시뮬레이션 우주론은 우주가 컴퓨터 시뮬레이션일 수 있다는 가설로, 물리적 법칙이 계산 가능한 알고리즘으로 표현될 수 있다는 아이디어에 기반합니다. 이 가설은 물리학, 컴퓨터 과학, 철학 등 여러 학문 분야에서 논의되고 있습니다. 리만 가설과 시뮬레이션 우주론의 관계는 다음과 같은 측면에서 논의될 수 있습니다.
- 복잡한 시스템의 모델링: 시뮬레이션 우주론에서 우주의 모든 현상은 수학적 알고리즘으로 설명될 수 있다고 가정합니다. 리만 가설이 해결되면 소수의 분포와 관련된 수학적 알고리즘이 더욱 명확해지고, 이를 통해 복잡한 시스템을 더 정밀하게 모델링할 수 있습니다.
- 정보의 구조와 분포: 리만 가설은 정보가 어떻게 구조화되고 분포되는지에 대한 이해를 돕습니다. 시뮬레이션 우주론에서는 우주의 모든 정보가 계산 가능한 방식으로 저장되고 처리된다고 가정하므로, 리만 가설의 해결은 이러한 정보 구조를 더 깊이 이해하는 데 기여할 수 있습니다.
- 우주의 기본 구조: 리만 가설의 해결은 물리학에서 기본적인 상수나 법칙의 이해를 높일 수 있습니다. 이는 시뮬레이션 우주론에서 우주의 기본적인 구조와 작동 원리를 이해하는 데 도움이 될 수 있습니다. 예를 들어, 소수의 분포와 같은 수학적 구조는 우주의 기본적인 특성 중 하나로 고려될 수 있습니다.
결론
리만 가설과 시뮬레이션 우주론의 관계는 직접적인 연결보다는 개념적이고 이론적인 연관성이 있습니다. 리만 가설이 해결되면 소수의 분포와 관련된 수학적 원리를 더 잘 이해할 수 있게 되며, 이는 복잡한 시스템을 모델링하고 정보 구조를 분석하는 데 중요한 역할을 할 수 있습니다. 시뮬레이션 우주론에서도 이러한 수학적 이해가 우주의 기본 구조와 작동 원리를 밝히는 데 기여할 수 있습니다.
'사회와 정치' 카테고리의 다른 글
| 은행법 전문 (0) | 2024.08.02 |
|---|---|
| [로즈웰 비행접시 사건] 마틸다 오도넬 맥엘로이의 외계인 에어럴 인터뷰 (0) | 2024.08.02 |
| 방통위 이진숙 후보 프로필 학력 나이 고향 (0) | 2024.07.24 |
| 미 대선 후보 카멀라 해리스 프로필 학력 나이 고향 주요 활동 (0) | 2024.07.22 |
| Area 51의 ufo 폭로자 밥 라자르 프로필 주요 발언(조 로건 팟캐스트) part 5(마지막) (0) | 2024.07.22 |



